Versegelung

Höhenanpassung

Bei einer Navigation mit der Sonne muss zwischen den Beobachtungen eine angemessene Zeit verstreichen, damit die Unterschiede zwischen den Sonnenständen groß genug sind und sich ihre Höhenkreise in einem genügend großen Winkel (möglichst >30°) kreuzen. Weil in der Zwischenzeit weiter gesegelt wird, verändert sich die Schiffsposition. Wenn die während der ersten Beobachtung festgestellte Höhe der Sonne auf den Ort der zweiten Beobachtung umgerechnet werden kann, dann hat man zum Zeitpunkt der zweiten Beobachtung gleichzeitig zwei Gestirne, eine eingebildete Sonne an der Position, in der sie während der ersten Beobachtung stand, und die wahre Sonne.

Zum Zeitpunkt der ersten Beobachtung wird die Sonne in der Höhe h beobachtet. Ihre Position am Himmel wird jetzt gedanklich fixiert. Wir betrachten diese gerade beobachtete Sonne bis zur zweiten Beobachtung als fiktives geostationäres Objekt und ebenso ihren  Bildpunkt auf der Erdoberfläche als fix. Infolge einer Ortsveränderung, einer Standort-Versegelung, wird sich der Abstand zum fixierten Bildpunkt ändern. Das Bild zeigt das in übertriebener Weise. Am Punkt B angekommen würde man den Horizontabstand der fiktiven Sonne in einer anderen Höhe hs messen. Da zu diesem Zeitpunkt auch die Höhe der weiter gewanderten wahren Sonne gemessen werden kann, liegen nun zwei Gestirnshöhen vor, woraus der momentane Standort bestimmt werden kann. Da die fiktive Sonne mit einem Sextanten nicht beobachtet werden kann, muss ihre Höhe auf den Ort B berechnet werden. Eine positive Änderung des Zenitabstandes \Delta s ist dabei gleichzusetzen mit einer negativen Höhenänderung: \Delta s=-\Delta h. Zur Berechnung dieser Höhenänderung hat der Niederländer Cornelis Douwes eine Formel angegeben. Sie lautet:

    \[\Delta h=\frac{d}{60}\cos (\text{c - z})\]

Zum besseren Verständnis dieser Formel dient das nächste Bild mit der fiktiven Sonne. Auch darin sind die Größenverhältnisse übertrieben dargestellt. COP1 ist der Höhenkreis der ersten Beobachtung der Sonne und wurde mit einem Zenitabstand s = 90° – h bei einem Azimut von z gemessen. Bis zur nächsten Beobachtung der Sonne vergeht Zeit und in dieser Zeit wird auf dem Kurs c eine Distanz von d zurückgelegt, der Standort wird versegelt. Würde nach dieser Zeit der Horizontabstand hs der fiktiven Sonne gemessen werden können, dann würde man ihren Zenitabstand als s‘ = 90° – hs erhalten und das ist der Radius des Höhenkreises COP1′. Dieser kann jetzt aber nur noch rechnerisch ermittelt werden. Die hier vorliegenden Gößenverhältnisse gestatten es durchaus, die Berechnung mit der Trigonometrie der Ebene durchzuführen. Da mit der versegelten Distanz d und dem abgesetzten Kurs c lediglich Schätzungen aus einer Koppelnavigation vorliegen, kann ohnehin nicht mit einer absoluten Genauigkeit gerechnet werden .

Um diese Höhendifferenz berechnen zu können, brauchen wir den Winkel zwischen der Differenzstrecke Δs und der versegelten Distanz d. Der Kosinus dieses Winkels liefert nach Multiplikation mit der versegelten Distanz die Differenz Δs der Radien und die ist gleich der Höhenänderung –\Delta h.

In dem im Bild gezeigten Beispiel kann der Winkel zwischen \Delta s und d nicht direkt angegeben werden. Stattdessen kann der 180°-Komplementwinkel \epsilon angegeben werden. Bei dieser Komplementregel gilt \cos (180^\circ-\epsilon)=-cos\, \epsilon, wobei \epsilon die Differenz von c – z ist. Dadurch erhalten wir für \cos(c-z) immer negative Werte, wenn sich der Radius der Höhengleiche aufgrund einer Versegelung vergrößert. Im umgekehrten Fall, wenn sich der Radius s infolge einer Versegelung verkleinert, sind die Werte positiv. Angewendet auf die Höhenänderung aufgrund von Versegelungen sind die Vorzeichen wegen \Delta h=-\Delta s genau umgekehrt. Diese Überlegungen führen auf \Delta h=d^\circ\cdot\cos(c-z).

Weil Höhen in Grad verwendet werden, muss zu diesem Zweck die in Seemeilen gegebene Distanz mit einer Division durch 60 in Grad verwandelt werden. Die Formel von Douwes ist also leicht nachvollziehbar.

    \[hs=h +\frac{d}{60}\cos (\text{c - z})\]

Dieser Vorgang nennt sich Höhenanpassung zur Berechnung eines versegelten Standortes. Die berechnete Radiusveränderung bewirkt dasselbe wie die Parallelverschiebung einer Standlinie bei den grafischen Navigationsmethoden.

Das Azimut

Die für die letzte Formel erforderlichen Angaben von d und c sind Ergebnisse einer Koppelnavigation, die entweder „zu Fuß“ oder mithilfe eines kleinen Programms ermittelt werden müssen. Das Azimut z ist vergleichbar mit einem rechtweisenden Kurs auf den Bildpunkt der Sonne. Rechtweisend Nord, es gibt auch ein rechtweisend Süd, bedeutet, dass der Winkel von einem nach Norden weisenden Meridian rechtsdrehend zu messen ist. Wir wollen jetzt das Azimut berechnen.

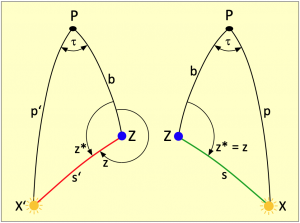Das nebenstehende Bild zeigt die zwei Polardreiecke XPZ und X’PZ. Darin ist das Azimut z zur Sonne der Winkel zwischen den Dreieckseiten b und s. Die Seite b ist jeweils der nördliche Abschnitt unseres Standortmeridians und die Seite s ist die Zenitdistanz 90° – h bzw. 90° – h’ unserer Sonnenbeobachtung. Die Seiten p und p’ sind die Meridiane der Sonnenbildpunkte X und X’. Weil das Azimut rechtweisend von unserem Standortmeridian aus gemessen wird, ist das Azimut mal ein Außenwinkel und mal ein Innenwinkel. Den Unterschied bestimmt dabei die Größe des LHA. Dieser ist der in westliche Richtung gemessene Längengrad-Abstand zwischen dem Standort und dem Bildpunktmeridian.
Am Schiffsmittag ist der LHA null, denn der Bildpunkt der Sonne passiert gerade den Standortmeridian. Der Bildpunkt wandert weiter und der westliche Stundenwinkel, in dem rechts dargestellten Dreieck als \tau bezeichnet, ist gleich dem LHA.
Um Mitternacht befindet sich die Sonne 180° von uns entfernt auf der gegenüberliegenden Seite der Erdkugel. Ab da nähert sich uns die Sonne wieder und der LHA vergrößert sich weiter. Der in dem linken Dreieck dargestellte östliche Stundenwinkel \tau verkleinert sich dabei. Seine Größe beträgt 360° – LHA. Am folgenden Schiffsmittag hat der LHA dann die Größe von 360° erreicht und zählt anschließend wieder von vorne.
Daraus ist nun abzuleiten, dass das Azimut von Mitternacht bis Mittag, wenn der LHA größer als 180° ist, als Innenwinkel am Polardreieck zu bestimmen ist. Vom Schiffsmittag an, bis in die dunkle Nacht hinein, ist das Azimut dann ein Außenwinkel.
Der Innenwinkel wird mit dem Kosinus Seitensatz gemäß Regel 2 auf Seite 85 berechnet. Die allgemeine Formel, auf die jeweils gemessene Höhe angewendet, lautet:

    \[\text{z*}=\arccos\frac{\sin\delta-\sin\varphi\,\sin h}{\cos\varphi\,\cos h}.\]

Da der Arkuskosinus nur Winkel zwischen 0° und 180° Grad liefern kann, sind damit sowieso nur Innenwinkel zu berechnen. Ein Außenwinkel an einem Dreieck ergibt sich einfach dadurch, dass der berechnete Innenwinkel vom 360° Vollkreiswinkel subtrahiert wird.
Wenn also der Bildpunkt den Standort überholt hat und Mitternacht noch nicht erreicht ist, dann ergibt sich das Azimut aus der Differenz von 360° und dem mit der Gleichung 4.13 berechneten Azimut-Innenwinkel. Mathematisch wird das folgendermaßen ausgedrückt:

    \[z=\left\lbrace\quad \;\;\;\phantom{100}z^*\;\;\text{wenn }LHA>180^\circ\atop 360^\circ-z^*\;\;\text{wenn }LHA<180^\circ\]

In der Zeit, als es noch keine Rechenmaschinen gab, wäre eine algebraische Berücksichtigung einer Versegelung über die Höhenanpassung nahezu unmöglich zu realisieren gewesen. Zur Berechnung des Azimuts braucht man die Standortbreite und den LHA. Letzterer ist wiederum nur über die Standortlänge zu bekommen. Das bedeutet nicht weniger, als dass zunächst am Ort der zweiten Beobachtung ein Standort komplett auszurechnen ist, und zwar ohne Berücksichtigung einer Höhenanpassung. Das Ergebnis wäre zwar ein recht nahe gelegener Standort, der aber weder der aktuelle Standort, noch der Ort der ersten Beobachtung ist. Er liegt irgendwo dazwischen. Mit der angepassten Höhe muss dann erneut in die Standortberechnung eingestiegen werden, um den aktuelle versegelten Standort zu erhalten.