Carl Friedrich Gauß und die analytische Auflösung

Johann Carl Friedrich Gauß war ein deutscher Mathematiker, Statistiker, Astronom, Geodät, Physiker und Elektrotechniker. Wegen seiner überragenden wissenschaftlichen Leistungen galt er bereits zu seinen Lebzeiten als „Princeps mathematicorum“. Gauß leitete in den Jahren 1821 – 1825 die Vermessung des Königreiches Hannover. Doch sein Interesse an der Landvermessung hatte er schon viel früher gezeigt.

Dabei benutzte er einen Sextanten, den er sich von seinem Freund Franz Xaver von Zach auslieh. Gauß war kein Seemann, doch eine Ortsbestimmung auf See unterscheidet sich nicht wirklich von einer Ortsbestimmung an Land. Schließlich muss auch ein Kartograf Längen- und Breitengrade auf seinen Landkarten einzeichnen können.

Gauß kannte die geometrische Lösung des Zweihöhenproblems sehr gut und wusste, dass diese, für eine Berechnung mit Logarithmen sehr aufwendig war, zu aufwendig, um in der Seefahrt verwendet zu werden.  So suchte er nach bequemeren Möglichkeiten.

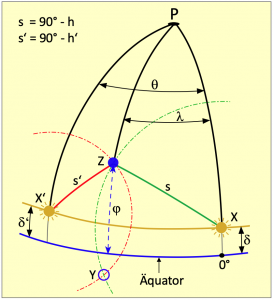
In dem nebenstehenden Bild kann jedes der zwei Polardreiecke XPZ und X’PZ mit einer Gleichung beschrieben werden. Weil beide Dreiecke die gemeinsame Seite PZ besitzen und darüber hinaus auch die Polwinkel über die Zenitabstände s und s‘ definiert sind, kann das, was die Zeichnung darstellt, auch mit einem Gleichungssystem ausgedrückt werden. Es war ein Mathematiker namens Kraft, der diese Idee als erster hatte. Allerdings bestehen beide Gleichungen des Systems aus den transzendenten Kreisfunktionen Sinus und Kosinus und für transzendente Gleichungssysteme gibt es keine Lösungsalgorithmen. So scheiterte der Mathematiker Kraft auch daran, eine praxistaugliche Lösung zu finden. Gauß gefiel dieser mathematische Ansatz und fühlte sich vielleicht herausgefordert. Er schrieb:

„Dieses alles beruhet auf rein geometrischen, freilich ganz einfachen Betrachtungen: es wird aber ohne Zweifel manchem angenehm seyn, eine directe Auflösung dieses Problems auf blos analytischem Wege entwickelt zu sehen wodurch sich aufs Neue bestätigen wird, daß alle Wahrheiten, welche aus geometrischen Betrachtungen abgeleitet werden, ebenso zierlich mit Hülfe der Analyse entdeckt werden können, wenn diese nur auf die rechte Art behandelt wird.“

Gauß wollte eine Lösung finden, bei der die Höhen zu beliebigen Zeiten gemessen werden können und er wollte auch gleich die Zeit berechnen, über die dann der Längengrad bestimmt wird. Die Auflösung des Problems bestand also im Finden der Unbekannten \varphi und \lambda des folgenden Gleichungssystems, welches das im vorstehenden Bild gezeigte geometrische Modell beschreibt:

\text{I: }\;\;\sin h=\sin \delta\sin \varphi+\cos \delta\cos \varphi\cos \lambda

\text{II:}\;\;\sin h'=\sin \delta'\sin \varphi+\cos \delta'\cos \varphi\cos (\theta-\lambda)

Gauß ist es gelungen, dieses Gleichungssystem zu lösen. Das Ergebnis bestand am Ende aus den Substitutionen F, V, W und G. Mit diesen Substitutionen konnten dann Breite und Länge des Standortes aus zwei Gestirnshöhen berechnet werden. Der Gauß Formelapparat ist letztlich gar nicht so kompliziert geworden und besteht aus den folgenden sechs Gleichungen:

(1)   \begin{equation*}F = \arctan\frac{\tan\delta'}{\cos\theta}\end{equation*}

(2)   \begin{equation*}V=\arctan\frac{\cos F\cdot\tan \theta }{\sin (F-\delta)}\end{equation*}

(3)   \begin{equation*}W=P\cdot\arccos\frac{\cos V\cdot\tan h}{\tan (F-\delta)}\bigg(\frac{\sin h'\cdot\sin F}{\sin h\cdot\sin \delta'\cdot\cos(F-\delta)}-1\bigg)\end{equation*}

(4)   \begin{equation*}G=\arctan\frac{\tan h}{\cos (V-W)}\end{equation*}

(5)   \begin{equation*}\lambda_0=\arctan\frac{\cos G\cdot\tan (V-W)}{\sin (G-\delta)}\end{equation*}

(6)   \begin{equation*}\varphi=\arctan\big (\cos \lambda_0\cdot\cot(G-\delta)\big)\end{equation*}

Hierin ist θ die Differenz der Greenwichwinkel aus beiden Beobachtungen, also θ = Grt‘ – Grt. Keine einzige dieser Formeln ist mit geometrischen Elementen erklärbar und auch \lambda_0 ist kein Stundenwinkel, sondern eine aus den Substitutionen V, W und G hervorgehende Standortlänge für den Sonderfall, dass die Seite PX der Nullmeridian ist. Das ist gewöhnlich nicht der Fall, doch dadurch berechnet sich die tatsächliche vollkreisige Länge immer nur aus der Summe

(7)   \begin{equation*}\lambda^{*}=\text{Grt}+\lambda_0\cdot\end{equation*}

Die sonst übliche Berechnung \lambda^\ast= Grt\pm\tau ist hier nicht angebracht, weil Gauß in seiner Analyse das zuerst beobachtete Gestirn auf dem Nullmeridian sieht und \lambda_0} somit stets das richtige Vorzeichen annimmt. Befindet sich der Standort auf östlicher Länge und beide Beobachtungen sehen die Sonne westlich, dann hat \lambda}_0 natürlich ein negatives Vorzeichen und so wird die Summe von Grt und \lambda_0} zur Differenz. Die geografische Länge \lambda} ist westlich, solange \lambda_0} kleiner als 180° ist. Sobald \lambda_0} 180° überschreitet, muss sein Wert von 360° subtrahiert werden und das Ergebnis sind Ostgrade.

Mit P wird vorgegeben, ob ein Standort nördlich oder südlich von der Deklinationsbreite berechnet werden soll. Für einen nördlichen Standort ist P = 1 vorzugeben und für einen südlichen Standort P = -1. Die Vorgaben +1 oder -1 sind aber noch mit dem Vorzeichen der aktuellen Deklinationsbreite zu multiplizieren. Soll beispielsweise ein Standort nördlich der aktuellen Deklination berechnet werden, dann gilt zunächst P = 1 für Nord. Wenn zu diesem Zeitpunkt die Deklination südlich ist, dann muss P = 1 mit -1 für südliche Deklination multipliziert werden und damit gilt P =  -1.

Wenn Beobachtungen an aufeinander folgenden Tagen erfolgen, dann muss mit der Besonderheit gerechnet werden, dass W je nach Zwischenzeit andere Vorzeichen annehmen kann und in der Folge ein Standort auf der falschen Halbkugel berechnet wird. Das zu verhindern, geschieht am einfachsten durch Anpassung des Vorzeichens des Polparameters P, der mit dem Gauß-Parameter W multipliziert wird. In seiner Grundform lautet P:

    \[P=\big(\text{if}\;\text{position}=N\;\text{then}\;1\;\text{otherwise}\,-1\big)\cdot\text{sign}\big(\delta\big)\]

Ohne weitere Beeinflussung von P werden Standorte auf der richtig gewählten Halbkugel theoretisch bis zur Mitte in das Folgedatum hinein berechnet. Damit Standorte auf der gewählten Halbkugel mit Zweit-Beobachtungszeiten nach beliebigen Tagen berechnet werden können, muss P durch Multiplikation mit folgendem Logikgausdruck korrigiert werden:

    \[\text{if}\;\text{dtime1}<\text{dtime2}\;\land\;\Delta t>0,4\;\text{then}\,-1\;\text{otherwise}\;1\]

Der angegebene Wert von 0,4 ist eine vorgegebene Zwischenzeit von 9,6 Stunden, wobei der Wert 1 einem 24-Stunden-Tag entspricht. Die Zahl 9,6 h ist willkürlich gewählt und ist die maximal zugelassene Zeit zwischen zwei aufeinanderfolgenden Beobachtungen.

Versegelungen werden dadurch berücksichtigt, dass die in der ersten Beobachtung gemessene Höhe h auf den Ort der zweiten Beobachtung angepasst wird. Das geschieht dadurch, dass h mit dmg° · cos(z – cmg) addiert wird (dmg = distance made good; cmg = course made good; z = Azimut). Das Ergebnis der Addition ist die versegelte Höhe hs , mit der dann alle Gleichungen bei W beginnend erneut berechnet werden müssen. Die Ergebnisse lauten dann Ws, Gs, \lambda_{0s}}, \varphi_s} und \lambda^*_s}, die dann in darauf folgenden Gleichungen verwendet werden müssen.

Wer sich intensiver mit der Gauß Analysis auseinandersetzen möchte, findet hier einen Ausschnitt aus der Original Gauß Publikation aus dem Jahre 1809 als pdf Datei: Gauß Methode.