Das Statement von Bobby Schenk

Revolution nach 500 Jahren bewährter Astronavigation?

gefunden in: https://www.bobbyschenk.de/n001/lops2.html

Man kann es kaum glauben, aber mit dieser Überschrift startet der Träger des internationalen OCEAN AWARD Bobby Schenk einen Beitrag, mit dem er gegen die auf dieser WEB-Seite vorgestellte App „sun-navigation“ und seinen Autor ziemlich unsachlich zu Felde zieht.

Was Herr Schenk in seinem letzten Satz schreibt, ist aber vollkommen richtig. Ich, Helmut Hoffrichter bin der Erlöser von ST. HILAIRE und SUMNER. Doch nur für diejenigen, die erlöst werden wollen oder müssen. Es gibt nämlich Segler, die sich für die astronomische Navigation interessieren, diese vielleicht als Backup an Bord haben möchten oder nur ab und zu mal mit einem Sextanten auf einer elektronischen Karte navigieren wollen, ohne sich dazu vorher einem Lernstress aussetzen zu müssen.

Wer mit der archaischen St. Hilaire Methode navigieren möchte und damit die Traditionen der Seefahrt pflegt, den halte ich keineswegs für schwachköpfig, wie Herr Schenk mir das unterstellen möchte. Leider gibt es aber auch Leute, für die es ein Sakrileg ist, wenn jemand nicht mit der Methode von St. Hilaire navigiert. Doch nach drei Jahrzehnten Satellitennavigation und einer ebenso langen stürmischen Entwicklung in der Computertechnik wird es Zeit, sich auch in der Astronavigation neuen Gegebenheiten zuzuwenden.
____________________
Habe ich richtig gelesen? “Revolution nach 500 Jahren bewährter Astronavigation“. Pardon, aber das ist entweder Weltvergessenheit oder Propaganda. Was sagt die Historie dazu?

Vor 500 Jahren hatte der Portugiese Pedro Nunes (1502 – 1578) die Vorstellung von zwei sich überschneidenden Höhengleichen und die Idee, dass einer der Schnittpunkte eine Beobachterposition sein müsse. Die Geschichte der Astronavigation kennt diesen Gedanken als Zwei-Höhen-Problem.

Am 17. Mai 1727 lobte die Pariser Akademie der Wissenschaften einen Preis für die Lösung des Zwei-Höhen-Problems aus. Zu dieser Zeit navigierte man mit dem Jakobsstab. Mittagsbreite und Nordsternbreite waren alles, was damit zu bestimmen war. Erst gegen Ende des Jahrhunderts fand man ein Modell zur geometrischen Bestimmung der Breite.

Da waren dann die ersten 300 der 500 Jahre rum, in denen sich die Astronavigation beständig in den Kinderschuhen befand und nach Lösungen suchte.

Carl Friedrich Gauß gelang 1809 eine vollständige analytische Lösung des Zwei-Höhen-Problems. Für seinen Lösungsweg benutzte er keine einzige Formel aus der sphärischen Trigonometrie. Seine Arbeit wurde deshalb nie zur Kenntnis genommen und ist bis heute unbekannt.

Am Ende der industriellen Revolution fuhren die ersten Dampfschiffe, aber die Navigation war noch immer nicht zufriedenstellend gelöst. Mit der geometrischen Methode konnten sich die Seefahrer nicht anfreunden, und Gauß ist gar nicht erst zu ihnen durchgedrungen. Dafür hätte man auch Rechenmaschinen gebraucht.

Die Erlösung kam 1837 mit der Entdeckung der Standlinie durch Thomas Sumner. Marcq Saint Hilaire optimierte dieses Verfahren 40 Jahre später für grafische Anwendungen. Es hat sich weltweit etabliert und wurde erst ganz am Ende des 20. Jhd. von der Satellitennavigation abgelöst. 

Somit gibt es keine 500 Jahre mit bewährter Astronavigation. Solange Veränderungen in einer Sache gesucht werden und solange Veränderungen in einer Sache stattfinden, hat sie sich nicht bewährt. Erst 1875 hat St. Hilaire ein Verfahren geschaffen, das sich weltweit etablierte und nun schon seit 150 Jahren bewährt, nicht aber seit 500 Jahren.

Was aber meint Herr Schenk mit der Revolution? Ich kann mir nur denken, dass er damit meine Arbeit meint, die vergessenen Navigationsmethoden und ganz besonders die von Carl Friedrich Gauß aus dem Schlaf zu holen und für die Seefahrer, insbesondere der künftigen Generationen, nutzbar zu machen. Sollte es eine Revolution sein, dann wurde sie bereits vor mehr als 200 Jahren vorbereitet.

____________________
Gleich im zweiten Absatz seines Statements musste ich dann erstmal lernen, dass ich Programme für Segler mache, „die die Sonne nicht von anderen Gestirnen unterscheiden können“, hört hört(!) und ich, anders als die traditionelle Astro-Navigation, „nicht die Methode von St. Hilaire“ verwende, sondern auf den Schnittpunkt zweier Höhengleichen setze.

Wie soll ich das bloß verstehen, was macht St. Hilaire denn anders? Er setzt doch auch nur auf die Schnittpunkte zweier Höhengleichen, nur eben handwerklich mit grafischen Hilfsmitteln, seinen Standlinien. Ich mache das rein rechnerisch, weil das endlich möglich geworden ist.

In nicht weniger als acht weiteren Absätzen wird dann versucht, den Lesern zu suggerieren, dass die Methode von Helmut Hoffrichter absolut untauglich ist. Damit das alle auch glauben sollen, gibt es keinen Link auf diese Webseite.

____________________
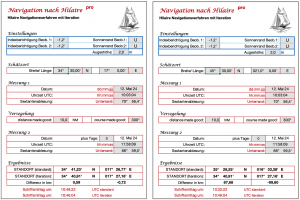
Weiter geht es dann mit dem Navigationsbeispiel, das ich mit meiner App „sun-navigation“ vorgetragen hatte. Das Standortergebnis lautet:

34° 40,85’ N / 017° 27,05’ E

Dieselben Daten verwendet Herr Schenk nun in seinem 30 Jahre alten PC-Programm Astro-Classic 2.0, muss zuvor aber noch die Sextantenbeschickung zurückrechnen, weil die von meiner App automatisch gemacht wurde und schreibt:

„Doch nun kommt St. Hilaire mit seinem System – mit dem der gesamte Schiffsverkehr aller Völker, die Weltumsegelungen (Erdmann, Pieske, Kammler, Koch usw.), die Rettung mittels Sextant von Apollo XIII („Houston, we have a problem!“), die Kabelverlegungen in den Ozeanen, leider auch die Luftschlachten der Alliierten und vor 1935 auch der Flugverkehr abgewickelt wurden.

„Ein Klick auf die braune Fläche – das Ergebnis erscheint!“ Fixort:

34° 41,2’ N / 017° 29,9’E

Beide Ergebnisse stimmen überein. Die Abweichungen betragen 0,31 NM in der Breite und -0,22 NM in der Länge.

Weil ich die Notwendigkeit eines Gissortes als lästig finde, reizt das Herrn Schenk mir zu zeigen, wie falsch ich damit liege. So wird ein Gissort eingegeben, der 1000 km weit vom Schiffsort entfernt liegt.

„Und siehe da: Selbst mit einem um über 500 Meilen falsch geschätzten Ort lag das Ergebnis nur etwa 1 Seemeile daneben – besser als in der Praxis oft nötig. Ein merkwürdiger Einwand von Hoffrichter ist das.“

Das ist jetzt aber nicht mehr klassisch!

Weil die St. Hilaire Methode ein Näherungsverfahren ist, wird damit kein Schiffsort bestimmt, sondern ein Ort, der sehr viel näher am Schiffsort liegt als der Gissort. Jetzt besteht die Wahl. Soll man diesen Ort als Schiffsort gelten lassen, oder soll man ihn als neuen Gissort definieren und damit den Standort neu und wesentlich genauer bestimmen. Mit Computern ist das ganz einfach, nennt sich Iteration und kann auch noch in weiteren Rechendurchläufen fortgeführt werden.

Mit der zweiten Option, kann der Gissort recht hemdsärmelig gewählt werden und die oft beschriebene Fehlerwahrscheinlichkeit bei der Messung und Verwendung großer Höhen ist auch nicht mehr vorhanden. Das Beispiel mit dem 550 NM weit entfernten Gissort, der nur eine Standortabweichung von 1 NM zur Folge hat, beweist ganz klar, dass Astro-Classic 2.0 gar nicht klassisch nach St. Hilaire arbeitet. Vielmehr handelt es sich um eine numerischen Positionsermittlung.

Das passt jetzt aber nicht zu diesem pathetisch vorgetragenen gesamten Schiffsverkehr aller Völker, den Weltumsegelern und alles was da oben sonst noch so aufgeführt wurde, denn die mussten alle mit dem echten klassischen St. Hilaire Verfahren klarkommen. Bei dem vorgegebenen „Phantasie Winkel“ und einer echt klassischen Standortbestimmung nach St. Hilaire betragen die Standortabweichungen in der Breite 88 km und in der Länge -100 km.

Das von mir angebotene Programm St.-Hilaire-pro, das hier zum Download steht, liefert zwei Ergebnisse. In der ersten Ergebniszeile erscheint der Standort so, wie er mit dem Original-St.-Hilaire-Verfahren bestimmt wird. In der darunter liegenden Zeile wird der Standort durch Iterationen numerisch berechnet. Der Nutzer wird also nicht getäuscht. Trotzdem muss immer ein Gissort eingegeben werden, und auch wenn das nur ein Phantasie-Gissort sein kann, finde ich das lästig.

____________________

Herr Schenk bemängelt: „Das Programm von Hoffrichter enthält keine Möglichkeiten wie sonstige Astro-Programme, nämlich: weder Mond, Fixstern und Planeten sind vorhanden“ und andere Dinge fehlen auch.

Die App „sun- navigation“ soll ja auch kein Astro-Programm wie andere sein. Nach drei Jahrzehnten Satellitennavigation ist es langsam unpassend, einer neuen Seglergeneration weiterhin ausschließlich die klassische Methode des letzten Jahrhunderts in voller Ausprägung aufdrücken zu wollen. Dieser klassischen Methode musste endlich eine Alternative zur Seite gestellt werden, die den täglichen Gewonheiten angepasst ist. Bis auf den Gebrauch eines Sextanten, sollte sie so einfach funktionieren wie Satellitennavigation, beispielsweise mit einer elektronischen Karte auf dem Display eines Mobiltelefons oder Tablets. Mond, Sterne und Planeten sind in einem Notfall nicht lebenswichtig und die Sonne reicht auch, wenn man mal gerade Lust dazu hat, mit einem Sextanten zu navigieren.

In der pro-Version besitzt das Programm von Hoffrichter ein Dead Reckoning Modul zur exakten Feststellung von Versegelungen und ein völlig unabhängiges zweites Navigationssystem, das mit beliebigen Einstellungen und beliebigen Eingaben parallel betrieben werden kann.

____________________

Am Schluss seines Beitrags überrascht mich Herr Schenk noch mit folgendem,  Zitat:

„Was nicht mehr lustig ist: Hoffrichter stellt auch gegentlich schlicht unrichtige Statements auf, wenn es der Verbreitung seines Programms dient. Dem Verfahren nach Sumner spricht er lässig die Fähigkeit ab, mit hohen Gestirns-Höhen zurecht zu kommen. Das ist schlicht falsch.“

Dazu betrachte man das Bild. In der Darstellung links ist die Sonne noch weiter weg und der Durchmesser der Höhengleiche ist groß. Bei Sumner müssen zwei Breiten und  gewählt werden, zwischen denen der Schiffsort vermutet wird. Für diese Schätzbreiten werden dann die Längen berechnet, woraus zwei Kreuzungspunkte am Ende des Kreisabschnitts entstehen. Durch diese Kreuzungspunkte wird nun eine Linie LOP1 gezogen, was dann eine Sekante ist. Diese Linie wurde einst „Sumnerlinie“ genannt und ist die Standlinie einer Gestirnsbeobachtung.

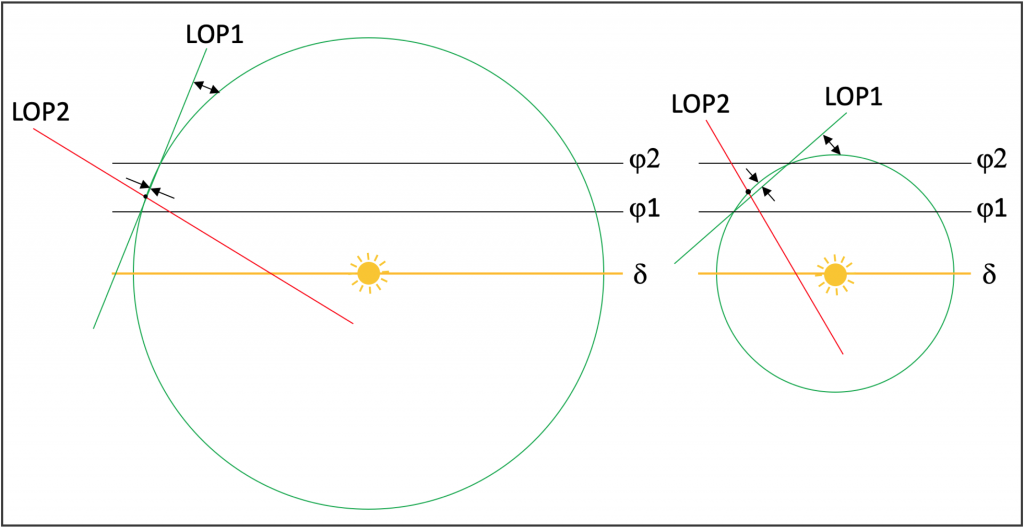
Die Sumnerlinie ist eine Gerade und die Höhengleiche ein Kreis. Also geht es nicht anders, es muss eine Erhebung des Kreisbogens über die Sehne hinaus geben, außer natürlich in deren Enden. Außerhalb des Kreises vergrößert sich der Abstand Standlinie-Kreislinie mit zunehmender Entfernung und besonders stark bei kleinen Kreisen. Diese Erhebung des Kreisabschnittes über der Sehne ist in dem Bild auf der rechten Seite größer, weil die Sonne viel näher und damit der Durchmesser der Höhengleiche viel kleiner ist. Auch wenn mit der Standlinie ein Stück Kreis angenähert wird, der Schiffsort ist immer ein Ort auf der Kreislinie und nicht auf der Standlinie, ein Dilemma bei allen Standlinienverfahren.

Folgt nun eine zweite Beobachtung, aus der eine zweite Standlinie LOP2 hervorgeht, dann wird der Schnittpunkt der Standlinien als Schiffsort berechnet. Dieser Schnittpunkt kann aber gerade dann, wenn Höhengleichen mit kleinen Durchmessern, also großen Höhen vorliegen, weiter weg von der Kreislinie selbst liegen, wie das im Bild rechts gut zu sehen ist.

Auf dem linken Bild ist kaum eine Erhebung zu sehen, die Standlinie ähnelt mehr einer Tangente als einer Sekante. Beim Hilaire Verfahren wird ja eine Tangente geradezu angestrebt. Aber auch dort kommt es bei Verwendung großer Höhen leicht zu Fehlern, denn die Standlinie aus der zweiten Beobachtung LOP2 kreuzt die erste Standlinie LOP1 immer außerhalb des Berührungspunktes der Tangente. Bei Sumner sind dagegen beide Kreuzungsvarianten möglich, also auch außerhalb der Sehne.